Page 28 - Azerbaijan State University of Economics

Murad Y. Yusıfov: Econometrıc Assessment Of Optımal Interest Burden: Case Study For Azerbaıjan

The results of statistical tests of the polynomial regression model (Annex A) pave
grounds to say that the model is adequate.

0,500

0,000

-0,500

-1,000

-1,500
Bank Profit_Lockdown (COVID-19)
Bank Profit_Non-Lockdown

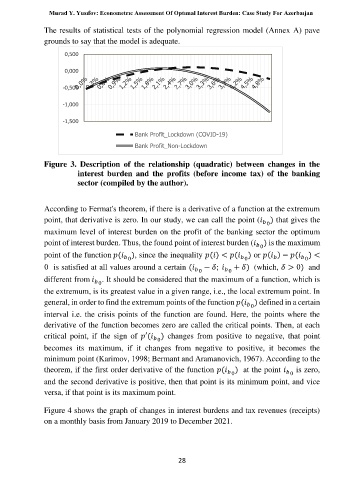
Figure 3. Description of the relationship (quadratic) between changes in the
interest burden and the profits (before income tax) of the banking
sector (compiled by the author).

According to Fermat's theorem, if there is a derivative of a function at the extremum
point, that derivative is zero. In our study, we can call the point ( ) that gives the

0
maximum level of interest burden on the profit of the banking sector the optimum
point of interest burden. Thus, the found point of interest burden ( ) is the maximum

0
point of the function ( ), since the inequality ( ) < ( ) or ( ) − ( ) <

0
0
0
0 is satisfied at all values around a certain ( 0 − ; 0 + ) (which, > 0) and
different from . It should be considered that the maximum of a function, which is

0
the extremum, is its greatest value in a given range, i.e., the local extremum point. In
general, in order to find the extremum points of the function ( ) defined in a certain

0
interval i.e. the crisis points of the function are found. Here, the points where the
derivative of the function becomes zero are called the critical points. Then, at each
critical point, if the sign of ′( ) changes from positive to negative, that point

0
becomes its maximum, if it changes from negative to positive, it becomes the
minimum point (Karimov, 1998; Bermant and Aramanovich, 1967). According to the
theorem, if the first order derivative of the function ( ) at the point is zero,

0
0
and the second derivative is positive, then that point is its minimum point, and vice
versa, if that point is its maximum point.

Figure 4 shows the graph of changes in interest burdens and tax revenues (receipts)
on a monthly basis from January 2019 to December 2021.

28